The Nautilus' Hull

de Neuville's Nautilus

The Nautilus' Hull

The Shape of the Nautilus

The chapter "Some Figures" presents this description of the Nautilus. As elsewhere I include Verne's French text and Lewis’s translation. Where necessary I've corrected or clarified Lewis:

« Voici. monsieur Aronnax, les diverses dimensions du bateau qui vous porte. C'est un cylindre très allongé, à bouts coniques. Il affecte sensiblement la forme d'un cigare, forme déjà adoptée à Londres dans plusieurs constructions du même genre. La longueur de ce cylindre. de tête en tête, est exactement de soixante-dix mètres, et son bau. à sa plus grande largeur, est de huit mètres. Il n'est donc pas construit tout à fait au dixième comme vos steamers de grande marche, mais ses lignes sont suffisamment longues et sa coulée assez prolongée, pour que l'eau déplacée s'échappe aisément et n'oppose aucun obstacle a sa marche.
« Ces deux dimensions vous permettent d'obtenir par un simple calcul la surface et le volume du Nautilus. Sa surface comprend mille onze mètres carrés et quarante-cinq centièmes ; son volume, quinze cents mètres cubes et deux dixièmes – ce qui revient à dire qu'entièrement immergé, il déplace ou pèse quinze cents mètres cubes ou tonneaux.

"Here, M. Aronnax, are the several dimensions of the boat you are in. It is an elongated cylinder with conical ends. It is very like a cigar in shape, a shape already adopted in London in several constructions of the same sort. The length of this cylinder, from stem to stern, is exactly 70 meters, and its maximum breadth is eight meters. It is not built on a ratio of ten to one like your long-voyage steamers, but its lines are sufficiently long, and its curves prolonged enough, to allow the water to slide off easily, and oppose no obstacle to its passage. These two dimensions enable you to obtain by a simple calculation the surface and cubic contents of the Nautilus. Its area measures 1011.45 square meters; and its contents 1,500.2 cubic meters; that is to say, when completely immersed it displaces 1500.2 cubic meters of water, or 1500.2 metric tons.

Original text from Zvi Har'El's Virtual Library

The description is a little contradictory and Verne's own illustrators show both a cigar or spindle shape and a cylinder with tapered ends. Having read about Ross Winans' cigar ships, I put great weight on the reference to the shape "adopted in London", a view Ron Miller also strongly advocates. The cigar ships were distinctly spindle shaped and I believe Verne visualized the Nautilus with this shape. Click this link for interesting details about the cigar boats.

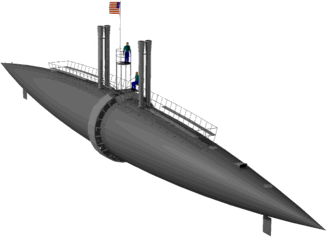
Let's examine the hull analytically, using the figures Nemo states in the text. (Incidentally, this material duplicates and extends a portion of Sylvain St-Pierre's extensive analysis, which inspired it.) To begin, Nemo may know the simple calculation he mentions, but I couldn't find one. We are given the length and the width, but the volume and area depend also on the shape. Figure 1 bounds the volume between two limits using shapes that do need only simple calculations. The larger volume, in orange, 2346 cubic meters, is an ellipsoid (actually a prolate spheroid). The smallest reasonable volume, in brown, would be 1173 for two back-to-back cones. Nemo's 1500 figure fits nicely between these.

Two simple shapes that bound the correct volume

Figure 1

Spheroid V = (4/3)

r_l r_s²
Two cones V = 2 (

/3) r² l

The Harper's Weekly article incorrectly identified the shape of the Winans steamer as paraboloid, an error repeated by later writers. Figure 2 shows the Nautilus hull formed of two end-to-end paraboloids. This is closer than the ellipsoid, but at 1759 cubic meters, still too large.

The hull formed by two paraboloids

Figure 2

Two paraboloids V = 2 (

/2) r² l

The Winans hull patent (#21917) gives the mathematical definition for its spindle shape as two intersecting circular arcs. Figure 3 shows such a spindle for the Nautilus dimensions. This shape is very pleasing, but what about the volume?

Figure 3

This is the result of some extensive mathematical gyrations. Unless I've transcribed them wrong the equations are correct, although they may be expressed differently or more efficiently. I had extensive education in math, but it was some time ago, and since my profession doesn't require very much exercise of the skill, I'm pretty rusty. Feel free to correct or inform me of better equations. The shape of the spindle hull is described by this equation, f(x):

y = (R² – x²)^½ - P for x between –s and +s

where
        R is the radius of the circle whose arc defines the hull shape
        P = R – r (r = maximum radius of the spindle)
        s = one half the length of the spindle

R is a function of the spindle radius and length:
R = ½ (r + s²/r)

For the Nautilus, whose radius is 4 meters and length is 70, R = 155.125.

Having the function f(x) for the spindle, its volume is calculated by this definite integral of the square of the function:

2 f ²(x) dx

We evaluate the integral between 0 and s and double the result because the spindle is symmetrical in x. I won’t go through all the gyrations to get here (it took forever to get the signs right), but the result is this (relatively simple) equation, that perhaps may be simplified further:

V = 2 ( 2 s³/₃ + P [ sP – R² sin^-1 (s/R) ] )

If this is the Nemo’s equation, it gives the wrong answer. The volume of a spindle of this size and shape is 1883.6 cubic meters, still too high.

It is possible to work backwards, given the volume, length and width, and assuming cones and cylinders. There are two unknowns, the cone and cylinder lengths, but two simultaneous equations that lead to a solution, shown in gray in Figure 4. The short central cylinder is only 9.8 meters long and the conical ends are 30.1 meters each.

Figure 4

V = 2 (

/3) r² l_cone +

r² l_cyl
L = 2 l_cone + l_cyl

The straight lines of this shape can be smoothed by combining the cylindrical center section with the cones and making a continuous curve. The hull shape becomes a more general rotational solid, created by rotating the resultant curve around the hull centerline. There is no simple volume equation for such a general solid, and the volume must be calculated by integration. As above with the spindle, a simple equation may result for a particular curve, and Nemo may have known it, but our task is more complicated. Starting with the correct value, the problem is smoothing the curve without changing the volume.

I approximated the integration process by dividing the hull into sections, calculating the volume of the sections, and adding them together. Mathematical integration works the same way but gives the true answer by using an infinite number of sections. Since the curvature is not great, using a small number of frustums, or truncated cones, yields a reasonable result. The volume of a frustum is calculated by a simple equation so it was easy to find a compliant shape by trial and error, checking the results of smoothing. The resulting shape is shown in Figure 4 in red. Other shapes also have the correct volume but they will all be very close to this one. It is surprising and very interesting that the hull shape is so slender. This has important ramifications in analysis of the Nautilus interior and layout.

Figure 5

Frustum V = (

/3) h (r_b² + r_br_t + r_t²)

Is this then the shape of the Nautilus? Well, maybe, but my own preference remains with the smoother spindle of the Winans boat. Compare de Neuville's drawing with the Winans steamer and with Figure 5. I will try to reconcile the differences in the discussion of the interior layout.

The Nautilus' Draft

In "Some Figures", Nemo specifies the displacement of the Nautilus (the Lewis translation is inexact):

« Lorsque j'ai fait les plans de ce navire destiné à une navigation sous-marine, j'ai voulu, qu'en équilibre dans l'eau il plongeât des neuf dixièmes, et qu'il émergeât d'un dixième seulement. Par conséquent, il ne devait déplacer dans ces conditions que les neuf dixièmes de son volume, soit treize cent cinquante-six mètres cubes et quarante-huit centièmes, c'est-à-dire ne peser que ce même nombre de tonneaux. J'ai donc dû ne pas dépasser ce poids en le construisant suivant les dimensions sus-dites.
…
-- Donc lorsque le Nautilus se trouve à flot dans ces conditions, il émerge d'un dixième. Or, si j'ai disposé des réservoirs d'une capacité égale à ce dixième, soit d'une contenance de cent cinquante tonneaux et soixante-douze centièmes, et si je les remplis d'eau, le bateau déplaçant alors quinze cent sept tonneaux, ou les pesant, sera complètement immergé. C'est ce qui arrive, monsieur le professeur. Ces réservoirs existent en abord dans les parties inférieures du Nautilus. J'ouvre des robinets, ils se remplissent, et le bateau s'enfonçant vient affleurer la surface de l'eau. »

"When I made the plans for this submarine vessel, I meant that nine-tenths should be submerged: consequently it ought only to displace nine-tenths of its bulk, that is to say, only to weigh that number of tons. I ought not, therefore, to have exceeded that weight, constructing it on the aforesaid dimensions.
…
"Then, when the Nautilus is afloat under these circumstances, one-tenth is out of the water. Now, if I have made reservoirs of a size equal to this tenth, or capable of holding 150 tons, and if I fill them with water, the boat, weighing then 1,507 tons, will be completely immersed. That would happen, Professor. These reservoirs are in the lower part of the Nautilus. I turn on taps and they fill, and the vessel sinks that had just been level with the surface."

Aronnax’s description of the deck in "The Black River" seems correct, but is in fact in error (I’ve corrected Lewis' mistranslation):

La plate-forme émergeait de quatre-vingts centimètres seulement.

The platform was only eighty centimeters out of water.

Original text from Zvi Har'El's Virtual Library

Look at the figure of three hull shapes viewed end-on. They all have the same physical dimensions, although the volumes of course are different. The one on the right is rectangular on all faces. 90% of the volume, nine tenths of the vertical dimension, is submerged. Three shapes showing exposed volume Eighty centimeters is exposed on the surface. This is the only case where 90% of the volume corresponds to 90% of the linear dimension. The center shape is a cylinder. Again 90% of the volume is submerged, but because the volume is concentrated around its long dimension, the hull rises about one and a quarter meters above the surface. The leftmost hull is spindle shaped. The volume is concentrated not only along the centerline but also amidships because the form is tapered. When 90% of the volume is submerged, the hull rises more than 1.6 meters above the water, twice the figure given by Aronnax. The three dimensional illustration at right may help to visualize the different volumes. (Note again that the three shapes as illustrated have different volumes. If the spindle length is 70 m, then a rectangular shape with the same volume would be 23 m long and the cylinder would be 29 m long.)

We might explain Aronnax's statement by assuming the ballast tanks were partially full, but the coincidence of the 80 centimeters is too strong. This is an error in Verne’s math.

The Structure of the Hull

Here is the description of the hull structure from "Some Figures". Again I've corrected Lewis:

« Le Nautilus se compose de deux coques, l'une intérieure, l'autre extérieure, réunies entre elles par des fers en T qui lui donnent une rigidité extrême. En effet, grâce à cette disposition cellulaire, il résiste comme un bloc, comme s'il était plein. Son bordé ne peut céder ; il adhère par lui-même et non par le serrage des rivets, et l'homogénéité de sa construction, due au parfait assemblage des matériaux, lui permet de défier les mers les plus violentes.
« Ces deux coques sont fabriquées en tôle d'acier dont la densité par rapport à l'eau est de sept, huit dixièmes. La première n'a pas moins de cinq centimètres d'épaisseur, et pèse trois cent quatre-vingt-quatorze tonneaux quatre-vingt-seize centièmes. La seconde enveloppe, la quille, haute de cinquante centimètres et large de vingt-cinq, pesant, à elle seule, soixante-deux tonneaux, la machine, le lest, les divers accessoires et aménagements, les cloisons et les étrésillons intérieurs, ont un poids de neuf cent soixante et un tonneaux soixante-deux centièmes, qui, ajoutés aux trois cent quatre-vingt-quatorze tonneaux et quatre-vingt-seize centièmes, forment le total exigé de treize cent cinquante-six tonneaux et quarante-huit centièmes. Est-ce entendu ?

"The Nautilus is composed of two hulls, one inside, the other outside, joined by T-shaped irons, which render it very strong. Indeed, owing to this cellular arrangement it resists like a block, as if it were solid. Its sides cannot yield; it coheres spontaneously, and not by the closeness of its rivets; and its perfect union of the materials enables it to defy the roughest seas.
"These two hulls are composed of steel plates, whose density is 7.8 that of water. The first is not less than two inches and a half thick and weighs 394.96 tons. The second envelope, the keel, which is twenty inches high and ten thick, and which itself weighs sixty-two tons, the engine, the ballast, the several accessories and apparatus appendages, the partitions and bulkheads, all together weigh 961.62 tons. When added to the 394.96 tons this yields the total 1356.48* tons. Do you follow all this?"

*This is a typo. The correct figure is 1356.58 - MC

Original text from Zvi Har'El's Virtual Library

One would expect a double hull design to have an inner pressure hull and an outer shell. Verne describes the details of one hull, but gives no further details about the other. Perhaps he means the described hull to be the pressure vessel, or perhaps the reference to homogeneity and a single block mean the combination of the both constitute the pressure vessel. If the first is true, is he describing the outer hull or the inner?

In his books, Ron Miller includes a small cross-section interpreting the hull structure. He specifies the outer hull thickness of about two inches, approximating the five centimeters noted in the text. His illustration gives about the same thickness to the inner hull and adds overlapping plates of that thickness atop the outer hull. His plans use a hull thickness of about 22 centimeters. The figure at left is my interpretation of Ron's drawing, with external rivets added to match his other illustrations. Click it to examine a hull section in 3-D.

F. W. Starr assumes the hull is a foot thick, about 28 centimeters, in the speculation published as an addendum to Philip José Farmer's Other Log of Phileas Fogg. In his plan 2, Greg Sharpe shows a hull thickness of about 30 centimeters and Gagneux uses about 27 centimeters.

I also used a relatively thick 20 centimeter hull structure for my original model. Now, trying to accommodate the full size of the salon, I've narrowed this down to less than twelve centimeters. I've shortened the T-iron and made some guesses about the mechanical structure. The result is illustrated at right and can be clicked to be examined in 3-D.

The example shows an outer pressure hull, or a combined structure. An inner pressure hull would reverse the thickness of the inner and outer plates and use a beefier T-iron.

Having settled on some possibilities for the hull, we can speculate on the layout of the Nautilus interior.

Do you have an opinion? Please e-mail me.